●「量子力学の観測問題、第3の解釈」（ボーム解釈）
2017/12/23
今回はタイムトラベルからずれてしまうが、量子力学の観測問題がテーマ。
まずはずっと気になっていた「EMドライブ」という未来の宇宙船用に研究されている新しい推進システムから。
●ついに燃料不要エンジン「EMドライブ」の謎が解明か？
2017/11/08 Nazolozyより
EMドライブ（wiki）はイギリスの航空宇宙技術者のロジャー・ショーヤー氏によって1997年に考案された推進システムで、内側に鏡を貼ったコーン型の容器にマイクロ波を反射させると推進力が生まれるという装置。
普通宇宙船のロケットエンジンは、推進剤を進行方向と逆に噴射してその反作用で加速する。このEMドライブは、そのような推進剤（燃料）を必要とせず太陽電池などでマイクロ波用の電力さえ供給できれば半永久的に加速し続けられる画期的なシステムだ。
中国やNASAなどでも研究されているそうだが、その原理に関しては不明のままで、運動量保存の法則に反しているという批判もある。
●EMドライブについての解説動画（英語 14：42）
The EM Drive: Fact or Fantasy? （Space Time）より
こちらは驚くべきことにルーマニアの大学のエンジニア、Berca Iulian氏が独自でEMドライブの実験に成功したという動画（まだ宇宙船にはほど遠い微弱な力だが・・・）。
●実際にEMドライブで推進力が発生したという実験動画（英語 6：30）
EmDrive Test No.03 Success, I have thrust !!!（iulian207）より
NazolozyによるとこのEMドライブの原理は量子力学の「パイロット波解釈」で説明ができるかもしれないという。
「パイロット波解釈」とは量子力学において量子が「粒子」と「波」の両方の性質をもつことを説明する解釈の一種。量子の2重性に関しては、こちらの動画がとてもわかりやすい。5分程度なのでぜひご覧を。
●2重スリット実験動画（英語/日本語字幕付 5：23）
2重スリットの実験（stcadioid）より
恥ずかしながら私はこの「パイロット波解釈」を知らなかった。
ネット情報通のある方からこの解釈について解説しているサイトを紹介してもらい、がぜん興味がわいた。
●量子力学の「観測問題」について
宇宙の謎を哲学的に深く考察しているサイト より
このサイトのテーマ「シミュレーション仮説」も興味深い。「ドッペルゲンガーの謎（3）」でも紹介しているが、どこかのタイミングでもう一度掘り下げてみたい。
量子の2重性に話を戻そう。
1つの粒子が波となって2つのスリットを通り抜け、スクリーンにぶつかったとき再び1つの粒子に戻るという「量子の2重性」を説明する解釈として、代表的なのは「コペンハーゲン解釈」だ。
●コペンハーゲン解釈（wiki）
量子力学の育ての親ともいわれるデンマークの物理学者ボーアを中心に提唱された理論で、観測される前の量子は波のように広がっており、観測された時点で波が収束して（波動関数の収束という）1つの粒子になるという考え方。
観測するのは人間でも実験装置でもかまわない。「コペンハーゲン解釈」という名前はボーアの研究所がコペンハーゲンにあったから。
2つ目は、「マルチバース」ブームにより再び注目されている「多世界解釈」だ。
●多世界解釈（wiki）
プリンストン大学の大学院生だったヒュー・エヴェレットが1957年に発表した論文が元になっているので「エヴェレットの多世界解釈」とも呼ぶ。
量子は観測された時点で可能性のある世界へそれぞれ分岐していくという考え方。
例えば2重スリット実験で観測された量子は、右のスリットを通った世界と左のスリットを通った世界へ分岐していく。分岐後の世界は互いに干渉できない。
※最初に多世界解釈を知ったときは、選択ごとに世界が増えていくなんて宇宙の無限増殖じゃないかと困惑したが、「パラレルワールドはあります！(2)」で紹介した、マルチバースは「実空間」には存在せず、確率によって枝分かれしていく「確率空間」に重なって存在するというカリフォルニア大学野村教授の「量子マルチバース」という考え方によって得心がいった。
3つ目はいよいよEMドライブの原理を説明することができるかもしれないという「パイロット波解釈」だ。
●パイロット波解釈（ボーム解釈）（wiki）
「パイロット波解釈」は、1952年にこの考え方を提案したアメリカの物理学者デヴィッド・ボームから「ボーム解釈」とも呼ばれる。
ただしこのボーム解釈、マイナーな考え方なのか数式を使わないで紹介しているサイトや本がなかなか見つからなかった。
その中でたまたま見つけたのが、サイエンスライター竹内薫氏の著書「図解入門よくわかる最新量子論の基本と仕組み」 だった。タイトルの通り量子力学についてとてもわかりやすく解説されており、第2章で「ボーム解釈」が詳しく紹介されている。
以下の考察は竹内氏の著書を参考にした。
まずこの「パイロット波」とは何か？
「パイロット波」は「ド・ブロイ波」とも呼ばれ、フランスの物理学者ド・ブロイに由来する。
ド・ブロイは、波と考えられていた光が粒子としての性質をもつならば、粒子と考えられていた物質も波としての性質をもつのではないかと考え、1924年に「物質波」というアイデアを発表した。
ボーム解釈では、目には見えないこの波がわれわれの世界に広がっていて、粒子は波乗りをするようにド・ブロイ波に運ばれていくという。
さて唐突だがここで量子力学の基礎となる次の方程式をご覧いただこう。
●シュレーディンガー方程式
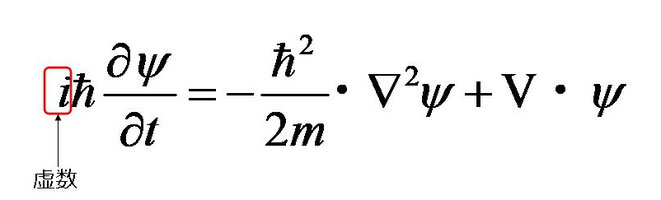
オーストリアの物理学者シュレーディンガーが1926年に先ほどのド・ブロイのアイデアをもとに考え出した方程式。
（私も含めて）数式にアレルギーのある方がいるかもしれないが、注目していただきたいのは左辺の「i」。
iは2乗すると-1になる虚数だ。英語では「imaginary number（想像上の数）」と呼ぶ。
この方程式は実数と、「i」という虚数が組み合わさった、複素数の方程式だということを覚えておいていただきたい。
シュレーディンガー方程式に
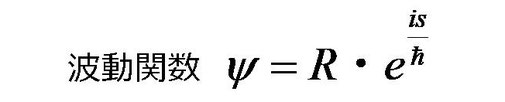
を代入して計算すると、次の式になる。
※式の計算は日本女子大学理学部の林教授の論文(10P）を参照。
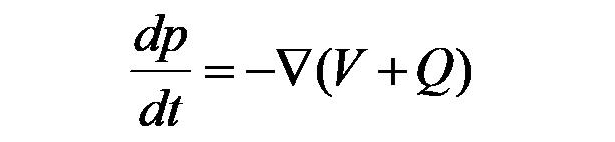
この式は古典的なニュートンの運動方程式にQを追加したものだ。
ちなみにQは「量子ポテンシャル」と呼び、こんな式になる。
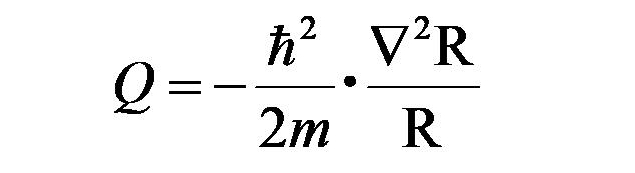
この「量子ポテンシャル」とはさきほどから「パイロット波」、「ド・ブロイ波」、「物質波」などのさまざまな呼び名で登場している波のことで、この上を粒子が波乗りしていく。
例えば2重スリット実験の「量子ポテンシャル」を図にするとこんな感じだ。
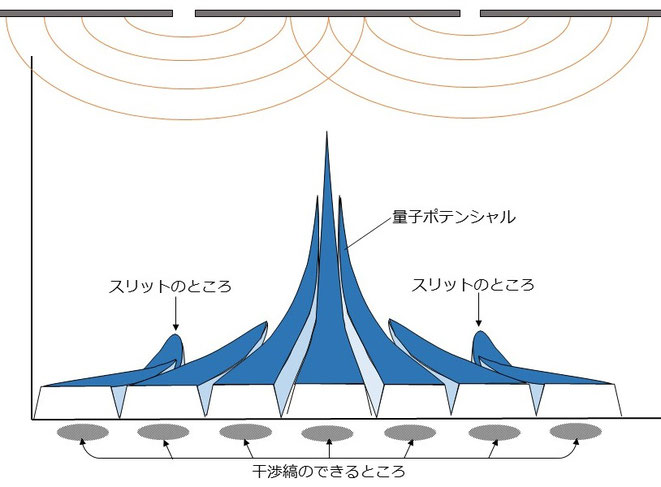
※実際に計算から算出された「量子ポテンシャル」は東京工業大学原子炉工学研究所の大崎氏の論文（39P）を参照。
2つのスリットの位置のポテンシャルが高くなっているが、中央が突出して高くなっている。
スリットに入った粒子はこのポテンシャルの波をビー玉が転がるように奥から手前へ波乗りしていく。そして手前のスクリーンにぶつかって干渉縞をつくるのだ。
コペンハーゲン解釈では発射された粒子が左右どちらのスリットを通るかはわからない。その途中は波として広がっていると解釈する。そしてスクリーンに衝突したときに再び粒子に戻る。
ボーム解釈の最大の特徴は、コペンハーゲン解釈では不明とされていた粒子がどちらのスリットを通ったのかという「経路」を説明できる点だ。ただし注意が必要だ。
ここで量子のもつ、もう1つの性質を説明しよう。
●不確定性原理
「不確定性原理」とはドイツの物理学者ハイゼンベルクが1927年に発表した量子の位置と運動量を同時に測定することはできないという性質。
数式では
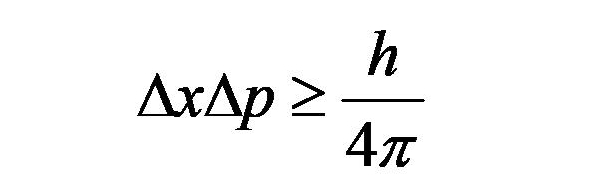
と表現され、xは位置、pは運動量を示している。xとpは反比例の関係にあり、どちらかを0に近づけていくとどちらかが無限大になってしまう。
ボーム解釈は経路を示すことはできるが、この「不確定性原理」により、粒子がどの経路を通ったのかを確定することはできない。
●トンネル効果
さて量子力学には量子が幽霊のようにある確率で壁を通り抜けてしまう現象もある。
これは「トンネル効果」と呼ばれ、量子コンピュータや一部のダイオードや顕微鏡などに応用されている。
次の図はコペンハーゲン解釈でのトンネル効果をイメージした図だ。
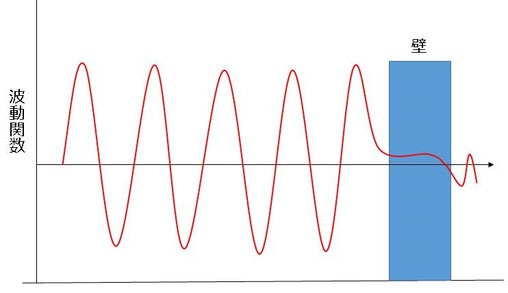
※竹内氏の著者「図解入門よくわかる最新量子論の基本と仕組み」
左から発射された量子が波（波動関数）となって壁にぶつかる様子を示している。
波動関数は「量子が観測によってその場所で発見される確率」なので、壁にぶつかる前の発見率が高いのは当然だが、トンネル効果によりわずかながら壁の右側にも発見される可能性があることを示している。
次の図はボーム解釈でのトンネル効果をイメージした図だ。
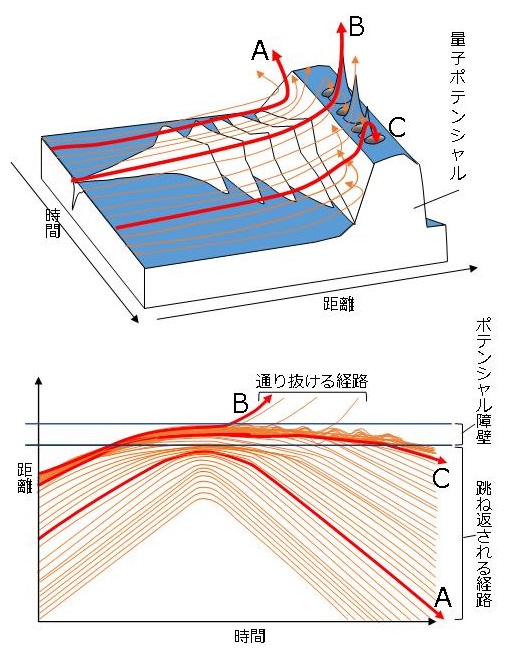
※竹内氏の著者「図解入門よくわかる最新量子論の基本と仕組み」
四角いはずの壁が、ボーム解釈の量子ポテンシャル上では、盛り上がったりトゲがあったり穴が開いていたりと複雑な形状をしている。
発射された量子は時間経過によってさまざまな経路を波乗りしていく。
例えばＡは壁にたどり着く前に量子ポテンシャルの盛り上がりに跳ね返されてしまう。
Ｃは盛り上がりを乗り越えたものの、量子ポテンシャルの穴にはまってしまい、手前に戻される。
Ｂだけが見事量子ポテンシャルのトゲをかけあがり、壁の向こうへ到達できるのだ。
トンネル効果においても、コペンハーゲン解釈では不明だった「経路」が、ボーム解釈ではどのような「経路」を通ったのか示される。
ただし不確定性原理により量子の出発点は不明なので、ボーム解釈でも「壁を通り抜けられる経路」を選ぶことはできない。
さてシュレーディンガー方程式に戻るが、なぜ「i」という虚数が重要なのか？
シュレーディンガー方程式を計算すればわれわれが住むマクロ世界になじんだニュートンの運動方程式が導かれるが、そこには虚数世界が隠されている。
量子ポテンシャルは目に見えないこの虚数世界に存在しているのかもしれない。
「虚数世界を図式化したものが量子ポテンシャル」というのがボーム解釈の真の醍醐味といえる。
さて今回ボーム解釈を考察してみて、あらためて数式を理解する重要性を感じた。
2018年は「タイムマシンやタイムトラベルの物理学を数式で説明できるようになる」を目標にしよう！