●多世界解釈の勘違い
2018/8/17
「量子（りょうし）」とは、光や電子といった素粒子などの物質やエネルギーの一番小さな単位だ。
このとても小さなミクロの世界を研究する「量子力学」では、普段われわれが目にするマクロの世界とは異なるさまざまな奇妙な現象が起こる。
その1つが量子は、粒子と波の2つの性質をもつことだ。
量子は普段は波のように空間に広がっており、場所を特定することができない。
観測されてはじめて「ここにある」と場所を特定することができるのだ。
実はここに量子力学が誕生してから続く解釈の問題が存在している。
今回のテーマは私がずっと「多世界解釈」に抱いていた「誤解」だ。
まずはこの問題を紹介するときに定番の「二重スリット実験」からはじめよう。
※量子力学に詳しい方はずっと下の▼まで飛ばしてください。
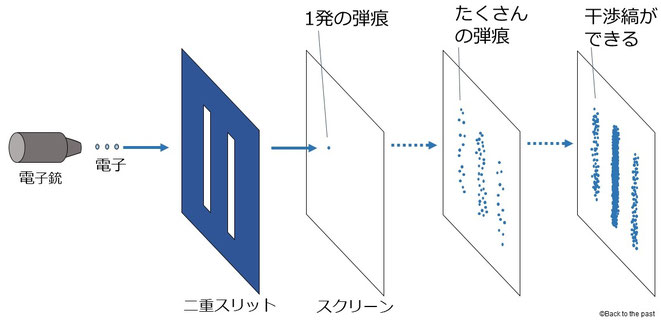
2つのスリット（隙間）が空いた板に向けて電子銃で電子を1発撃つと、スリットを通り抜けた先のスクリーンに弾痕が1つ刻まれる。
これは不思議でもなんでもない。
次に2発目を発射する。スリットを通り抜けた電子は、スクリーンの最初とは異なる場所に2発目の弾痕を刻む。
続けてたくさんの粒子を発射していくと、スクリーンには干渉縞（かんしょうじま）と呼ばれる縞模様が浮かびあがる。
この干渉縞は波と波がぶつかったときにできる特徴的な縞模様だ。
この実験の結果を簡単に説明すると、電子は1発ずつでは粒子的な性質をもつが、それが集まると波の性質が現れるのだ。
この不思議な性質は電子だけでなく、光子や、さらにフラーレンという原子60個が集まった大きな分子でも干渉縞が現れる。
つまりわれわれを構成するすべての物質は、波でもあり粒子でもあるのだ。
ではいつ波が粒子に変わるのか？
冒頭で「普段は波のように広がった量子が、観測されると場所が特定される」と書いたが、この波のように広がった状態のときに量子のいる場所は、「ψ（プサイ）」という「波動関数（波の関数）」で「どのあたりにいそうか？」という確率でしか示すことができない。
そしてこの波の状態は、「シュレディンガー方程式」という方程式によって決まる。
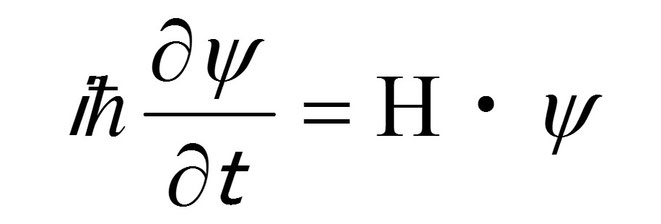
このシュレディンガー方程式は、波動関数の広がる空間（ヒルベルト空間と呼ばれる数学的な空間）で時間の経過に従って波動関数が未来にどのように変化していくのかを教えてくれる。
この方程式を考案したシュレディンガーは、いつ波が粒子に変わるのかについて、有名な猫を使った実験を考案した。
中の見えない箱に1匹の猫と放射性物質、それに毒ガス入りのビンとある装置を入れる。
この装置は放射性物質が崩壊したらガイガーカウンター（測定装置）が感知して、毒ガスのビンが割れて中の猫が死んでしまう仕組みになっている。
放射性物質がいつ崩壊するかは確率的にしかわからないので、外からは猫が生きているのか死んでいるのかわからない。
つまり中の猫は箱を開けて確かめるまで、生きている状態と死んでいる状態が重なった状態といえる。
シュレディンガーは猫が嫌いでこんな残酷な実験を思いついたのではなく（あくまでも思考実験なので、想像上の実験だ）、ミクロの世界（放射性物質の崩壊）でしか起こらないとされる波動関数の収縮をマクロ世界の問題（猫の生死）として定義したのである。
では再び元の質問に戻ろう。
ではいつ波が粒子に変わるのか？
これにはさまざまな解釈がある。
代表的な解釈として、箱の中が見えない状態では、猫は生死の重なった状態になっており、箱を開けてはじめて生死が確定される。つまり広がった波が観測してはじめて粒子として1つの場所に収束される。
この考え方を「コペンハーゲン解釈」と呼ぶ。
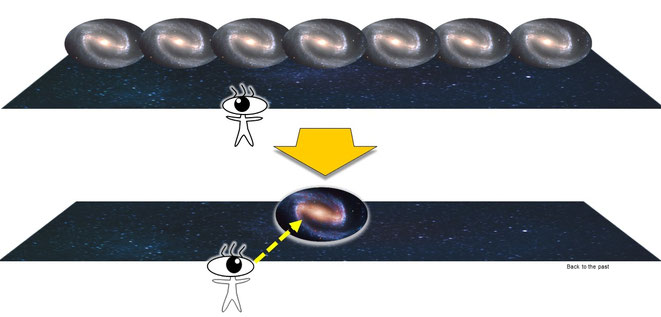
※コペンハーゲンとは、このアイデアを1920年代に考案した量子力学の父、ニールス・ボーアの所属していた研究所がデンマークのコペンハーゲンにあったことにちなむ。
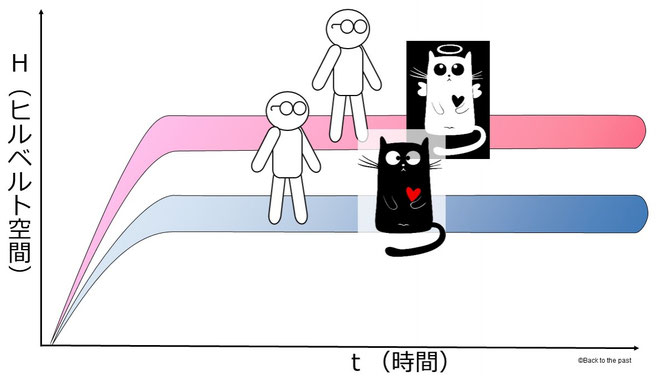
他の解釈として最近注目を集めているのが、箱の中の猫は死んでいる状態（下図の赤）と生きている状態（下図の青）が重なったまま、われわれがそれぞれの世界に分岐していくという考え方だ。
これを「多世界解釈」と呼ぶ。
この多世界解釈は1957年にプリンストン大学の大学院生だったヒュー・エヴェレット3世によって考案された。
しかしエヴェレットがこの仮説を発表したときにはほとんど支持を得ることができず、物理学の研究を続けることなく大学を去ってしまった。
しかし最近では永久インフレーションからたくさんの宇宙が生まれるというマルチバース理論や並行宇宙の考え方を支持する科学者が増え、多世界解釈の支持も広がっている。
例えば並行宇宙の研究で有名なマサチューセッツ工科大学のマックス・テグマーク教授が、1997年のメリーランド大学の会議で48人の物理学者にとったアンケートでは、コペンハーゲン解釈支持が27％だったのに対し多世界解釈支持は17％だったが、2010年にハーバード大学での講演で35名を対象に行ったアンケートではコペンハーゲン支持が0％に対し、多世界支持は46％にもなった（マックス・テグマーク「数学的な宇宙」「数学的な宇宙
究極の実在の姿を求めて」
※このアンケートでは対象者の母数が少ないので似たような調査を探したところ、2016年に行われたデンマークのオーフス大学による8つの大学1234名の研究者を対象に行った調査を見つけた。
この調査によると、コペンハーゲン支持は39%、多世界支持は6％で、依然コペンハーゲン支持が大勢を占めているが、支持を決めかねている人も36％いる。
興味深いのは多世界解釈に関して65%の研究者が「パラレルワールドは存在する」と答えている。
※▼
さて今回のタイトルは「多世界解釈の勘違い」である。
私がコペンハーゲン解釈と多世界解釈を知ったときしっくりきたのは、重なり合った波が観測によって粒子となるとき、波動が1つに収縮するよりも、2つの世界にわかれていくというイメージだった。
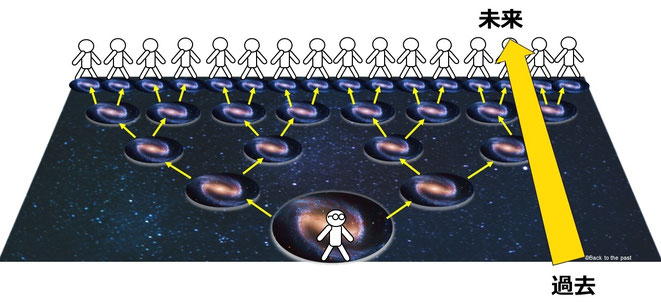
ただし多世界解釈に対して疑問もあった。
観測とは人間の目による以外にも、機械による観測や他の物質と相互作用することも含まれる。
四六時中観測ごとに分岐しまくって世界が増えていったら「例え宇宙がどんなに広くとも、やがて許容量がいっぱいになるのではないか？」、「そもそもそんな増殖する世界を作るエネルギーはどこから来るのか？」と不思議に思っていた。
だがエヴェレットのオリジナルのアイデアはこのイメージとずいぶん違っていた。
ある方から私の勘違いを指摘され、この度あらためてエヴェレットの論文「“Relative State” Formulation of Quantum Mechanics」を読んでみた。
エヴェレットが主張していたのは世界が2つに分岐することではなかった。
そもそもエヴェレットは「多世界」という言葉を論文では使っていない。
※「多世界」という言葉は1970年代にそれまで無視され続けていたエヴェレットの論文を再評価したブライス・ドゥイットによって命名された。
エヴェレットの元々のアイデアは、量子力学における(1)波動関数の収縮と(2)時間経過の2つのプロセスにうち、(2)の時間が進んでいくことだけで説明できないかという試みだった。
さらに観測者を外に置かず、世界の中に入れてしまった。
重なりあった可能性は収縮することなく、そのままずっと可能性として残っていく。
そして観測者は、シュレディンガー方程式によって選択されたどれかの世界の中の記憶に属していくのだ。
これは簡単にいえば、広大な宇宙の中に無数の可能性があって、観測者は方程式に従って選ばれた可能性を進んでいくイメージだ。
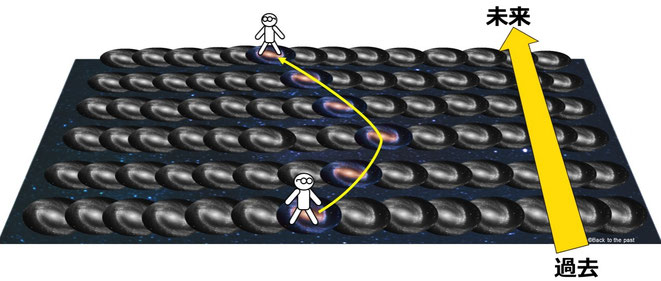
あらゆる可能性は最初から重なり合って大きな1つの全体の中にあるので、可能性の数は無限ぐらいあっても許容量オーバーにはならず、最初からあるので新たに産み出すエネルギーは必要ない。
こうして私の懸念は払拭された。
ちなみにエヴェレットの論文には「m」という関数が出てくる。
このmを、エヴェレットは可能性の「重み付け」として使っている。
起こりうる「世界の数」、簡単に言えばある事象の「起こりやすさ」だ。
シュレディンガーの猫を使って下記の図で説明すると、青色の世界が赤色より多い、つまり猫が生きている世界の数が多いので、猫が生きている確率が高くなる。
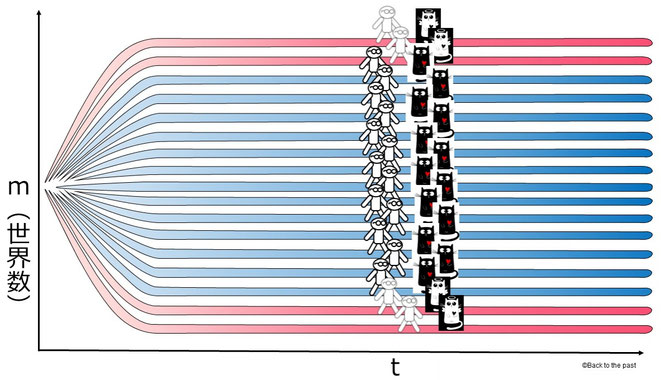
エヴェレットの多世界解釈のメリットは、波動関数の収縮を考えないので、どこまでが「ミクロ」でどこからが「マクロ」かというあいまいな区分をしなくてすむ。
また観測者は世界の中に含まれるので、観測者を分離することなく統一の世界で解釈できる。
デメリットは、方程式によって選ばれなかった世界を観測する方法は現在のところ見つかっておらず、実験によって検証できないことだ。
ただし多世界解釈でもコペンハーゲン解釈でも、結局シュレディンガー方程式に従うので、計算結果はどちらも変わらない。
最後にこのサイトのテーマ「タイムトラベル」と「多世界解釈」について簡単に触れておきたい。
多世界解釈でのタイムトラベルの最大のメリットは、現在より過去や未来を進むパラレルワールドへの移動となるので、「親殺しのパラドックス」や「情報起源のパラドックス」を避けられることだ。
※詳しくは「ホーキング博士とタイムトラベル」を参照
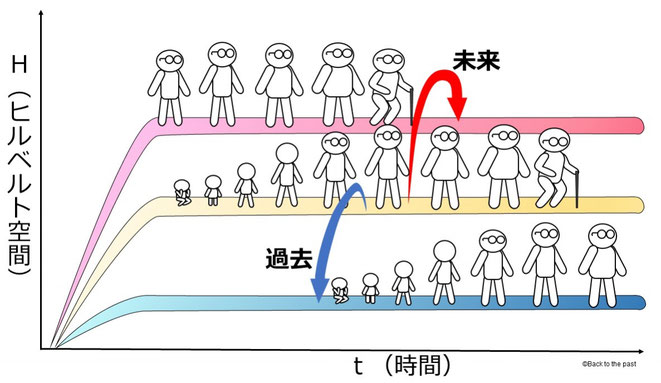
エヴェレットの多世界解釈を研究していると、時間の流れは幻想かもしれない「スポットライト理論」や「離散的な時間」との共通点が浮かんでくる。
このあたりを追求していくと疑似科学に広がってしまうため、「タイムトラベルネタPICK UP!」であらためて考察してみたい。