●世界初！画像にとらえられた「量子もつれ」と「ベルの不等式」の解説
2019/8/5
今年（2019年）4月、世界ではじめてブラックホールの撮影に成功したとして話題になったが、
今度はなんと「量子もつれ」の瞬間が撮影された！
ただしこの「量子もつれ」、ブラックホールほど有名じゃないのでよくわからないという方も多いはずだ。
今回はそもそも「量子もつれとは何なのか？」、それが「どのようにして撮影されたのか？」について解説してみたい。
まず「量子もつれ」とは何なのか？
今回の重要なキーワードは「ベルの不等式」とその破れだ。
「どのようにして量子もつれが撮影されたのか？」早く知りたい方はこちら▼をクリック。
まず「量子もつれ」とは物質を構成する素粒子のようなミクロな世界を研究する「量子力学」で、あのアインシュタインをして「不気味な遠隔作用」と言わしめた。
2つの粒子を用意してもつれさせ、どんなに遠く離したとしても、片方の粒子を観測した瞬間、もう一方の粒子の状態が確定する不思議な現象だ。
え？ どこが不思議かわからない？
恋人同士に例えて説明しよう。
アリスとボブがいて、アリスが念願の宇宙飛行士になり、地球から10光年先（光の速さで10年かかる距離）の惑星まで宇宙旅行したとする。
目的の惑星にたどり着いたアリスは、出発前にボブから渡されたペンダントを開けた。
ペンダントの中には量子もつれ状態の光子（光の粒子）が入っている。
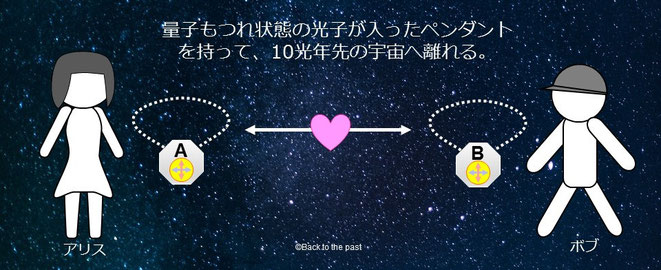
光子はスピンという角運動量（回転する自転のような運動）を持っており、縦（垂直方向）または横（水平方向）のどちらかにスピンしている。
ペンダントを開けるまでは縦と横のスピンが重なった状態でどちらかわからない。
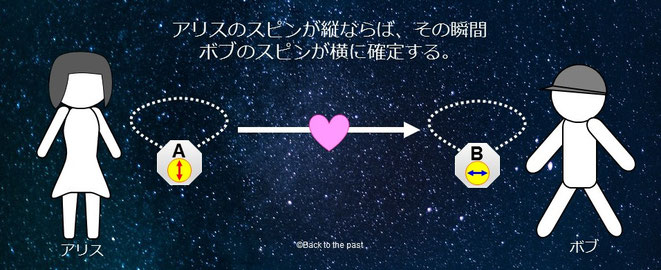
アリスがペンダントを開けると光子のスピンは縦だった。その瞬間、地球にいるボブの光子のスピンが横に確定するのだ。
10光年も離れているのにアリスが光子のスピンを観測したとたん、ボブの光子のスピンが瞬時に確定したのは、「2人の愛が時空を超えて、2つの光子のスピンを伝えたのだ」というのが量子もつれである。
※実際は2人の愛は量子もつれに関係ない。
これはすごい現象だ。量子もつれを使えば、将来「10光年離れていてもリアルタイムで会話が可能な超光速通信ができるじゃないか」と思われるかもしれないが、残念ながらそれはできない。
ペンダントの中のスピンの方向はランダムなので、好きなように決めることができない。相手のスピンが自分のと逆だとわかるだけで、これを使って互いに情報をやりとりすることは不可能なのだ。
また、どんなに離れていても情報が瞬時に伝わるのだから、アインシュタインが提唱した「この世に光より速い速度はない」という特殊相対性理論に反してないか？
実際に「量子もつれは量子力学がまだ不完全な証拠だ」という論文を、アインシュタインはポドルスキー、ローゼンという物理学者と共同で1935年に発表した。
※（3人の名前の頭文字をとって）EPRパラドックスと呼ばれる。
中身を観測するまで「2つの状態が重なっている」というのが量子力学の主張。いやいや重なっているんじゃなくて、はじめからどちらかの状態に決まっているが、見えないだけで「隠れた変数が存在するんだ」というのがアインシュタインの主張だ。
そこでこの隠れた変数を見つける式をアイルランドの物理学者ジョン・ベルが考案した。
ベルが1964年の論文の中で発表した式を「ベルの不等式」と呼ぶ
|C(A,B) + C(A',B) + C(A',B'）- C(A,B'）|≦2
※ベルの不等式はいろいろな形があり、これはその中の１つCHSH不等式(1969年)。
アリスのペンダントの光子が縦の場合A、横の場合A'、ボブのペンダントの光子が縦の場合B、横の場合B'とする。
アリス縦（A）、アリス横（A'）、ボブ縦（B）、ボブ横（B'）を4つの扉と見立て、扉の奥にはそれぞれ+1か-1の数字が隠れている。
アリスはAかA'の扉のどちらかを、ボブはBかB'のどちらかを選んで開ける。
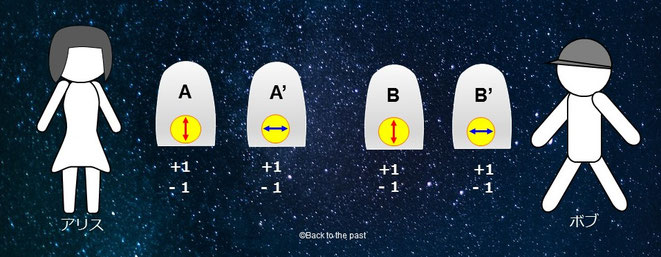
【ルール１】
それぞれの扉の奥に隠された数字が一致すれば+1ポイント、不一致ならば-1ポイント。
(例1）アリスがAの扉を開け数字は+1。ボブがBの扉を開け数字は+1・・・一致しているので+1ポイント
(例2）アリスがAの扉を開け数字は+1。ボブがBの扉を開け数字は-1・・・不一致なので-1ポイント
【ルール２】
2つ目のルール、アリス扉（A）とボブ扉（B'）の組み合わせを選んだときだけ、中の数字が一致したら-1ポイント、不一致ならば+1ポイント。
(例3）アリスがAの扉を開け数字は+1。ボブがB'の扉を開け数字は+1・・・一致しているので-1ポイント
(例4）アリスがAの扉を開け数字は+1。ボブがB'の扉を開け数字は-1・・・不一致なので+1ポイント
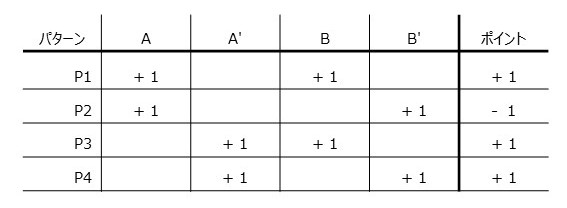
アリス（A）、アリス（A'）と ボブ（B）、ボブ（B'）の扉の数字の可能性をすべて書き出すと、
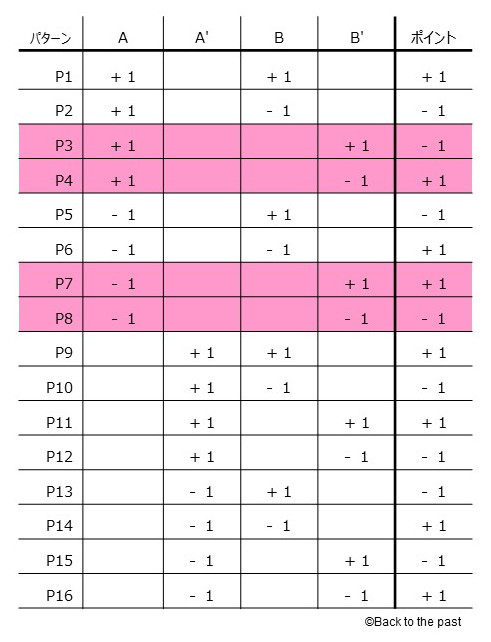
注目したいのはピンク色の網をかけているアリス扉（A）とボブ扉（B'）の組み合わせ。
このときだけ、ルール2より獲得ポイントが他の組み合わせと逆になる。
ここで、2人の獲得するポイントがなるべく大きくなるようにした場合、期待値はどこまで大きくなるだろう？
※期待値とは1回の試行で得られる値の平均値のこと。「得られる値」×「それが起こる確率」をすべて足したもの。
例えばAからB'までの4つの扉すべてに隠された数字が確率100％で+1の場合、組み合わせは、
{(A,B/+1ポイント）×1/4｝+{(A,B'/-1ポイント)×1/4} + {(A',B/+1ポイント）×1/4｝+{(A',B'/+1ポイント）×1/4)｝=(1/4)-(1/4)+(1/4)+(1/4)=1/2
4つの扉の数字が常に+1のときの期待値は1/2となる。
実はどんなに調整しても、期待値を1/2より大きくすることはできない。
なぜならアリス側の扉の数字とボブ側の数字のかけて足し算すると、
(A×B)+(A'×B)+(A'×B')-(A×B')= (A+A')×B+(A'-A)×B'
ここで、(A+A')と(A'-A)の組み合わせをすべて書き出すと
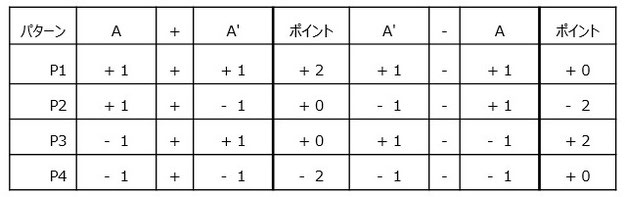
(A+A')と(A'-A)のどちらかが0で、どちらかが-2または+2になる。
つまり、
-2≦{(AB)+(A'B)+(A'B')-(AB')｝≦2
※×の記号は省略
両辺に確率1/4をかけると、
1/4{(AB)+(A'B)+(A'B')-(AB')｝≦1/2
よって、期待値が1/2より大きくなることはない。
ちなみに
{(AB)+(A'B)+(A'B')-(AB')｝≦2
は「ベルの不等式」になっており、左辺をSと置くと、
S={(AB)+(A'B)+(A'B')-(AB')｝≦2
つまり隠れた変数があってS≦2ならば不等式が成り立つが、ベルは論文の中で
量子力学ではS＞2になり、不等式が破れる（成り立たない）ことを示した。
これを1982年にフランスの物理学者アラン・アスペが実験で証明した。
高校で習うsin、cosなどの三角関数を使うので計算は省略するが、
(AB)=√2/2、(A'B)=√2/2、(A'B')=√2/2、(AB')=-√2/2 になり、
S=(√2/2)+(√2/2)+(√2/2)-(-√2/2)=2√2
2√2は2.828427･･･なので S＞2、つまりベルの不等式は破れた。
量子は重ね合わせの状態になっており、隠れた変数などないことが証明されたのだ。
さて、こんな奇妙な現象を実際にどうやって撮影したのか？
今回イギリスのグラスゴー大学の研究チームによって撮影に成功した量子もつれの画像がこちらだ。
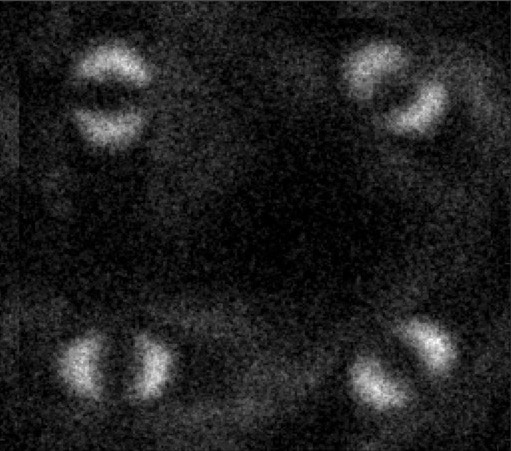
ポール=アントイン・モロー、エルメス・トニネリ、トーマスグレゴリー他
2019/7/12 Science Advancesより
研究チームはもつれた光子の相関関係を調べるのに、スピンの角運動量（縦か横）ではなく、軌道角運動量（OAM）を使った。
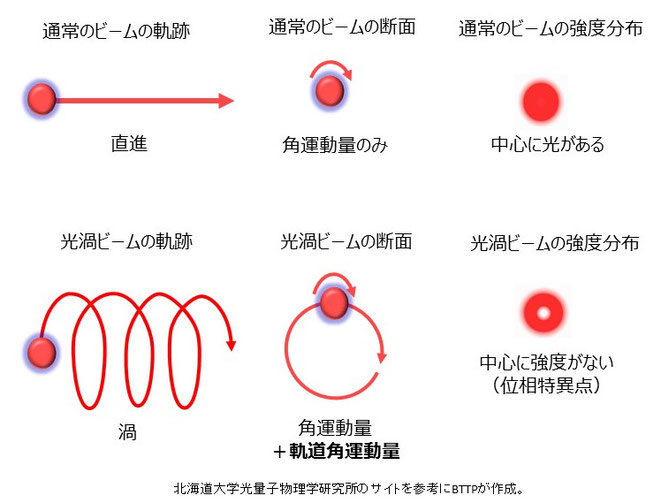
軌道角運動量(OAM）とは、光が「光渦（ひかりうず）」と呼ばれるねじれた渦巻き状に進むときに発生し、スピン（角運動量）を自転とすれば、公転的な動きだ。
※2次元のスピン（角運動量）ではなく3次元の渦（OAM）を使った理由として、より高次元でテストしたほうが、もつれた光子の画像の解像度をあげられるからだ。
実験の概要は、
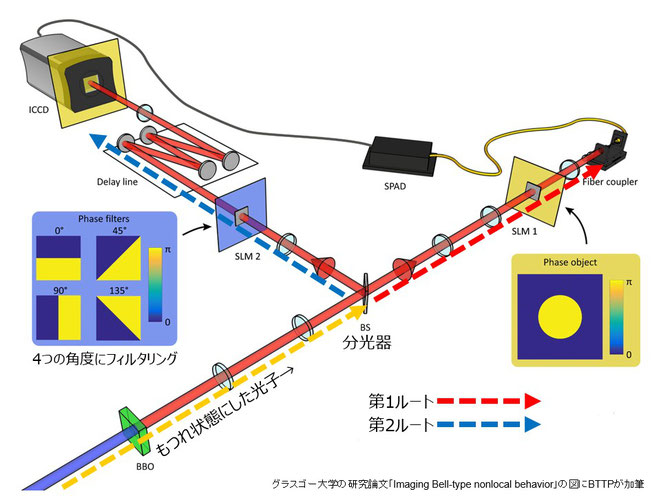
自発的パラメトリック下方変換（SPDC/wiki）という方法で、まず、もつれ状態にした光渦を分光器で第1ルート、第2ルートの2つに分けた。
第1ルートを進む光は単一のフィルター（SLM1）で位相を変えずに進む。
第2ルートには通過の際に4種類の角度（0°，45°，90°，135°）に変化するフィルター（SLM2）が設置されている。
第1ルートには、単一の光子（1ピクセル当たり1光子）の画像を撮影するためにSPADという検出器を設置し、2つのルートを通った光子を超高感度（ICCD）カメラで同時に撮影する。
それぞれのルートの光をフィルターの角度（0°，45°，90°，135°）ごとに円対称の位相イメージで記録し、合計で40,000の光子の画像を撮影して合成した。
結果としてそのイメージがベルの不等式S≦2を破っていれば、量子もつれの画像を撮影したと言える。
まず4つの角度（0°，45°，90°，135°）にフィルタリングされたイメージを、それぞれの角度ごとに撮影した。
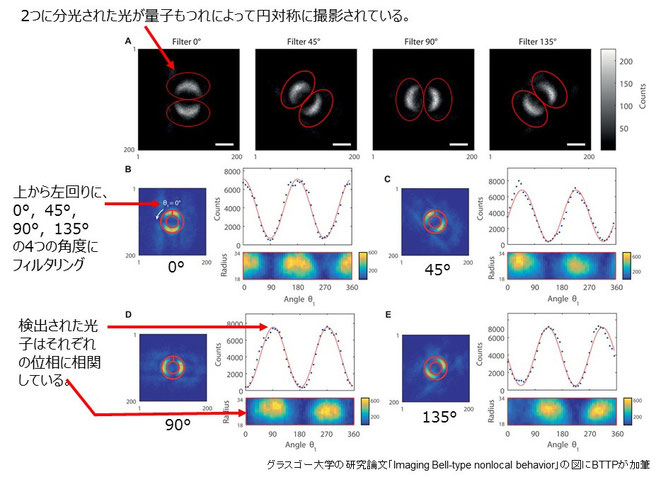
円対称の縁に沿って「リング状の興味深い領域（ROI）」の画像が浮かび上がった。
これらの画像をもとにベルの不等式を計算したところ、S=2.4626±0.0261であり、ベルの不等式S≦2を破っていた。
次に4つのフィルタリングを単一の画像内におさめるように調整し、それぞれのフィルタリングはランダムで撮影した。
撮影した画像を重ねて合成したところ、
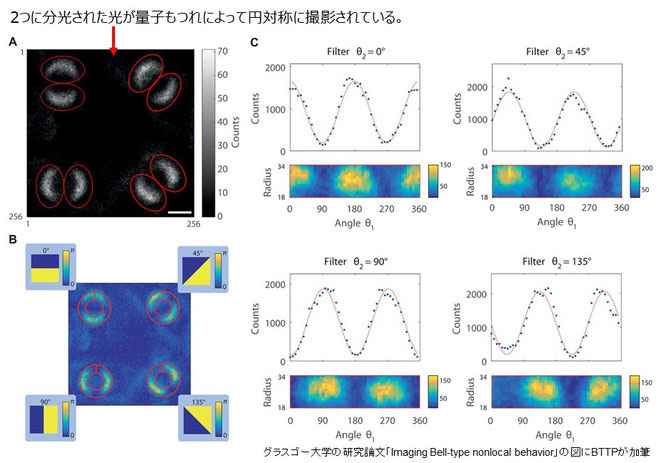
見事に4つの角度ごとに円対称になった画像ができあがり、こちらも S=2.443±0.038でベルの不等式S≦2を破った。
研究チームによるとこの実験にはまだ不完全な部分もあるが、技術の進歩によって将来的に解決できるという。
この実験の目的は量子もつれを画像化することで、量子コンピューティングをはじめとしたさまざまな「量子もつれ現象」のパフォーマンスを推し量るベンチマークにすることだ。
いままで数字上でしか評価できなかった「量子もつれ」を視覚化することで、今後新たな発見につながることを期待したい。
【Reference】
●Bell の不等式が成立しない理由を（できるだけ）平易に説明してみる
めもめもより