●時間が遅くなる仕組みとは？
2018/4/13
※この原稿はNazologyに掲載いただいた『SF映画の数式がイラストでわかる！「タイムマシンの物理学」』に加筆したものです。
このサイト「Back to the past」を立ち上げてから約2年、未来人やタイムリープといったタイムトラベルに関する話を集めて「それが本当の出来事ならば、どんな仕組みなのか？」を考察してきた。
しかしタイムトラベルと真剣に向き合えば向き合うほど、物理学を「数式で理解することの大切さ」を痛感してしまった。
映画「バック・トゥ・ザ・フューチャー
(字幕版)」
だが私のように数学が苦手で高校や大学でまともに物理を学んでいなかったものは、この「数式」が最大の敵となる。
やる気を出して書店を探しても、並んでいるのはまったく数式を使わない初心者向けの「入門書」か、理系の学生や研究者向けに書かれた数式満載の「専門書」だ。
文系人が「専門書」を開くと、読み方のわからないギリシャ文字や専門用語、サイン・コサイン・微分・積分といったトラウマ的な言葉が襲いかかり、芽生えかけた意欲も吹き飛んでそっと本を閉じてしまう。
だが私のような文系人でも「数式を交えて物理を理解したい」、「いつかはオリジナルの理論を数式で説明したい」と夢見る奇特な人もいるかもしれない。
そんな人のために、なるべくシンプルでわかりやすい物理の数式解説ができないかと思いついた。
テーマを「タイムマシン」にしぼり、網羅的な知識は他のサイトや書物に譲る。本格な理論の導出をしようとは思わないし、そんな実力もない。
私がしたいのは、物理や数学は苦手だが、SF小説や映画でタイムトラベルやタイムマシンに興味をもち、「どんな数式を使えばそれが実現できるのか？」を知りたい人のための解説だ。
文系人の私だからこそできる数式へのアプローチがきっとあるはずだ。
うまくいくかはわからないが、とりあえずチャレンジしてみよう！
さて最初のテーマだがタイムマシンといえば、まずこれだ。
「時間が遅くなる仕組みとは？」
その前に、昔は「時間が変化しない」と思われていたことから説明したい。
いまでこそ時間は相対的なもので、あなたにとっての「今」と私にとっての「今」は違うことがわかっているが、100年ちょっと前までは「時間は絶対的なもの」だと信じられていた。
世間の認識がひっくりかえったのは1905年にアインシュタインが特殊相対性理論を発表してからだ。
アインシュタインによれば「時間（や空間）は相対的で変化するもの」なのだ。
でもアインシュタインが突然「時間が相対的なもの」というアイデアを思いついたわけではない。
アインシュタインがすごいのは、いままで変化すると思われていた光の速度を「変わらない唯一の速度」と定義したことだ。
そして光の速度に近づくほど時間の進み方が遅くなるとした。
※このあたりを説明するために普通は光を媒介すると考えられていたエーテルやマイケルソン・モーリーの実験を紹介するのだが、私はシンプルにいきたいのでバッサリ省略する。気になる方は検索してください。
さっそく「時間の遅れ」を計算する数式を紹介しよう。
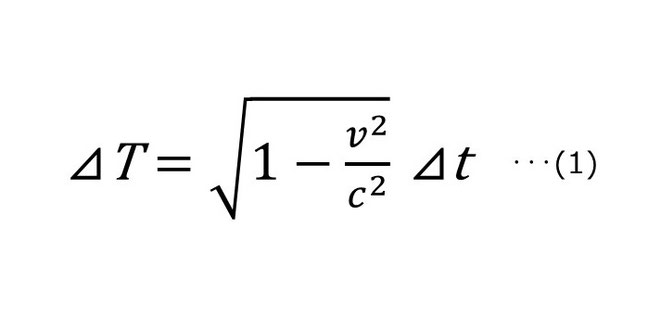
文系人はまず読み方がわからないとムズムズするはずなので左から説明すると、⊿（デルタ）は「ごくわずか」、tは「時間（time）」、vは「速度（velocity）」、cは「光の速度（constant/定数）」を意味する。
右のごくわずかな時間ｔにルートの中をかけると、左のごくわずかな時間Tに変換されるという式だ。
※なぜわざわざごくわずかな時間にしているかと言うと、瞬間的な時間であればその間の速度変化を考えなくてよいので、お手軽な慣性系で計算できるからだ。
(1)の式を日本語で解説すると、
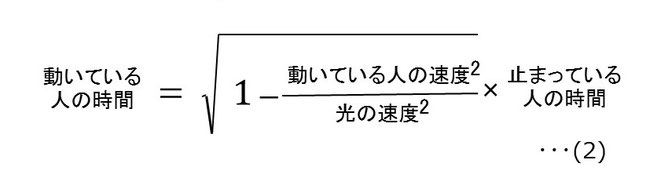
どうだろう？ 少しはわかりやすくなっただろうか？
なかなかイメージできない？ それではこの式がどうやってできたのか説明しよう。
最初にアインシュタインの話をしたので難しそうな特殊相対性理論を使うのかと思いきや、なんと中学校で習うピタゴラスの定理（三平方の定理）から説明できる。
次の図を見て欲しい。
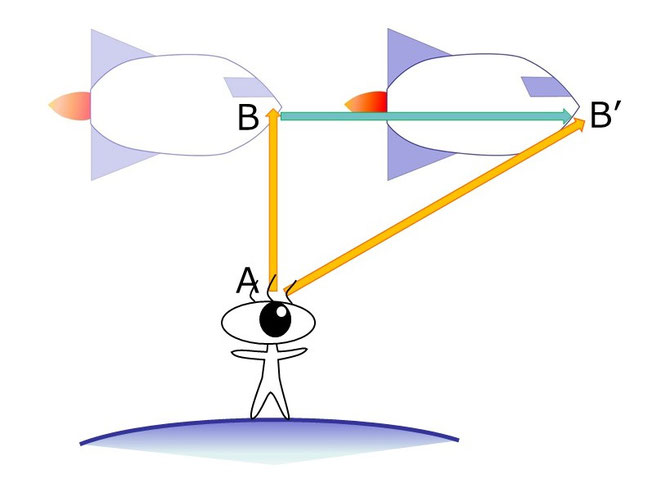
地球にいるAさん（止まっている人）から、ロケットに乗って光の速度（30万km/秒）に近いスピードで飛んでるＢさん（動いている人）を見たとしよう。
Ｂさんのロケットがvの速度で飛んでいて、BからＢ’の位置までくるのにt時間かかったとするとB－B’間の距離は「道のり＝速さ×時間」だから「vt」と表わすことができる。
ちなみにA－B’間の距離は、Aさんが観測する光の速さcとBからB'までの時間tをかけたものだから「ct」。
残ったA－B間の距離は、止まっているAさんから動く前のBの位置にいたロケットまでの時間をTとすると、光の速さは不変なのでさっきのcを使って「cT」となる。
上の図に書き込むと、
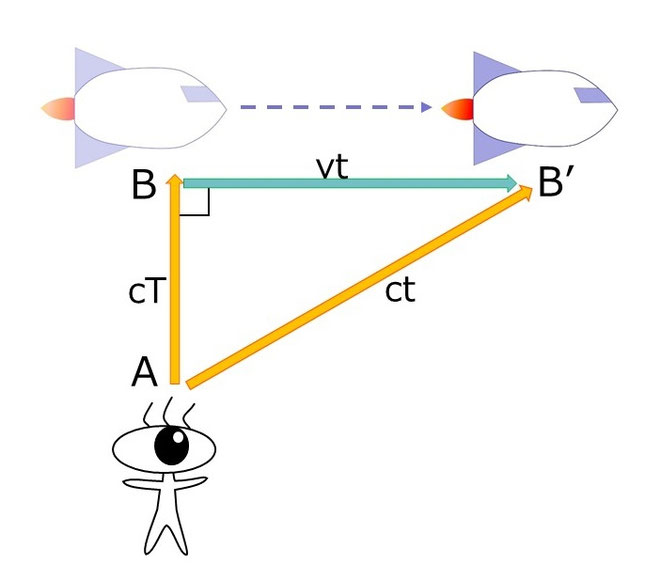
注目したいのはcT間の距離にくらべ、ct間の距離が斜めに延びていることだ。
光速度不変の原理よりc（光）の速度は変わらないので延びた分だけ時間が遅くなってしまう。
この理屈がわかったら、次はピタゴラスの定理を思い出そう！
上の三角形△ABB’はBが直角の三角形なので斜辺AB’はピタゴラスの定理から次のように計算できる。
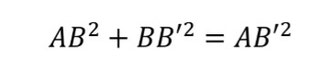
辺ABを「cT」、辺BB’を「vt」、辺AB’を「ct」に置き換えて計算すると、
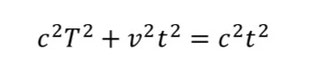
両辺からv2t2を引くと
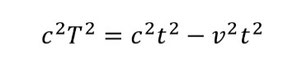
両辺をc2で割ると、
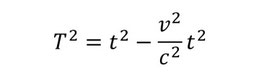
右辺のt2を（ ）でまとめて、両辺に正の平方根をとると
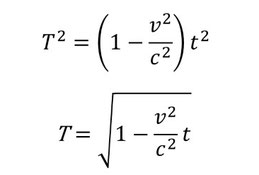
ほら(1)の式になった！
それではいよいよ時間の遅れを計算してみよう。
日本語の(2)の式に具体的な数値を入れてみる。
光の速度は約30万km/秒、Bさん（動いている人）のロケットはその2/3の速さ20万km/秒で飛んでいるとする。地球にいるAさん（止まっている人）からすると、
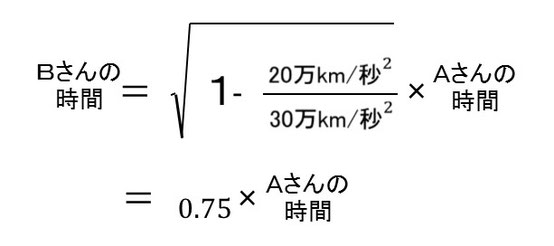
つまりAさんの時間の進み具合はBさんに比べて75％になる。言い換えるとAさんはBさんより1.3倍時間が遅れる。
(2)の式の「動いている人の速度」を変えていろいろ入力すれば、どのくらい時間を遅くできるのかがわかる。
つまり光速度の10％（3万km/秒）ぐらいでは時間はほとんど遅れず、10倍の遅れを体感するには光速度の99.5％（29.85万km/秒）というとんでもないスピードが必要とされる。
実感するだけの時間の遅れを実現するのは、なかなか難しい。
せっかくここまで読んでいただいたので、光の速度に近づいていくと起こるもう一つの奇妙な現象をご紹介しよう。
なんと光の速度に近づくにつれて物体の長さが「縮む」のである。
まず「縮み」を計算する数式をご紹介しよう。
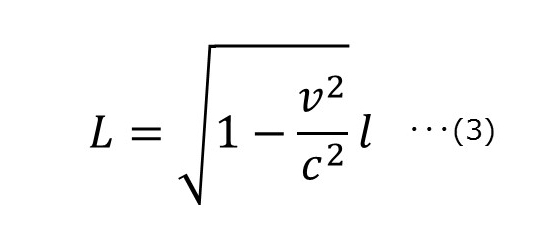
(1)の「時間の遅れ」の計算式とよく似ている。
引き続きロケットを例にして説明すると、左からLは「飛んでいるロケットの長さ（Length）」、vが「ロケットの速度」、cが「光の速度」、そしてｌが「静止しているロケットの長さ」を意味する。
念のため(3)を日本語にした式と、V（ロケットの速度）を変えればどれくらい「縮むのか？」を計算してみよう。
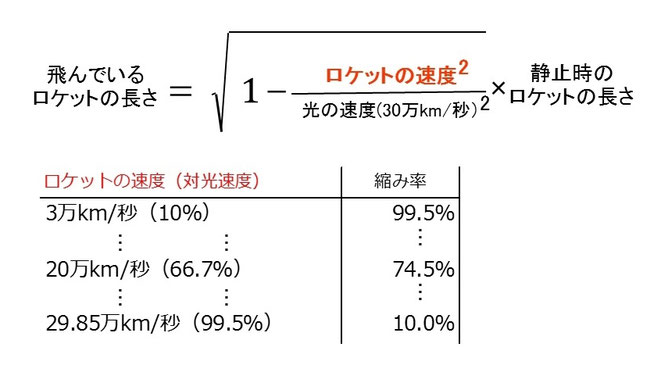
「時間の遅れ」と同じで「縮み」を実感するにはかなりのスピードが必要なようだ。
この計算を図にすると
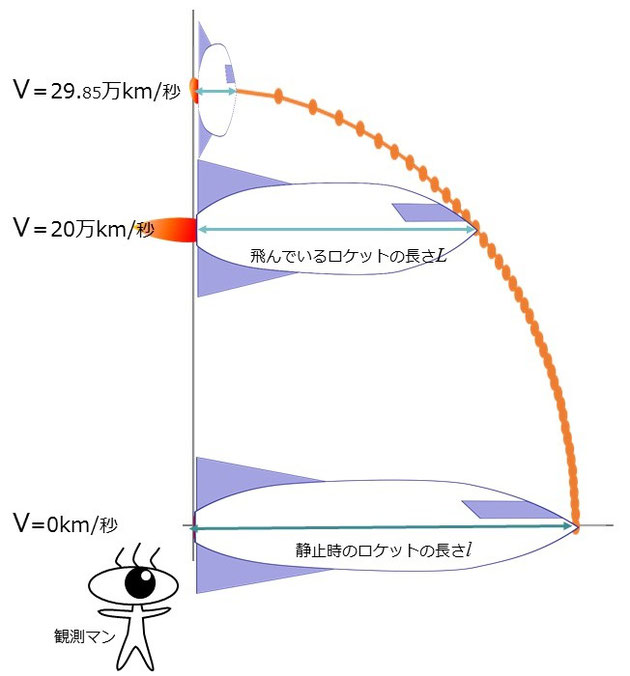
V（ロケットの速度）が光の速度（30万km/秒）に近づくにつれ、急激に縮んでいくことがわかる。
ここで（3）の式を導いてみよう。大丈夫、そんな難しい計算は使わない。
静止したロケットの長さlと光の速度cと地球からロケットを見ているAさん（「観測マン」と名付けよう）の時間tとの関係は「道のり＝速度×時間」から、
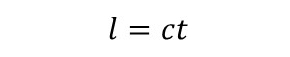
ｔについて解くと
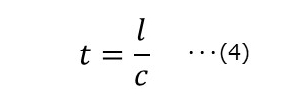
次に、飛んでいるロケットの長さLと光速度c、ロケットに乗っているBさんの時間Tとの関係は、
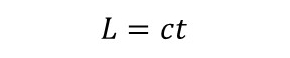
Tについて解くと
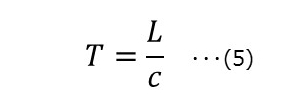
(4)・(5)を「時間の遅れ」の計算式
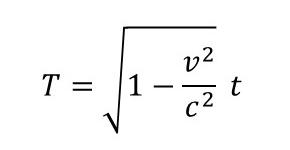
に代入すると
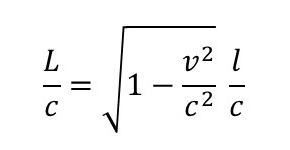
両辺にcをかけて
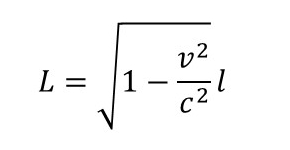
となり、簡単に(3）の式を導くことができた。
この式は考案したオランダの物理学者ヘンドリック・ローレンツ（wiki）にちなんで「ローレンツ収縮」と呼ばれている。
最後にクイズを出そう。
ロケットに乗っている人から見たら、地球にいる観測マンは「伸びて見える？」 それとも「縮んで見える？」
・・・
・・・・・・
・・・・・・・・・
・・・・・・・・・・・・
答えは下の図
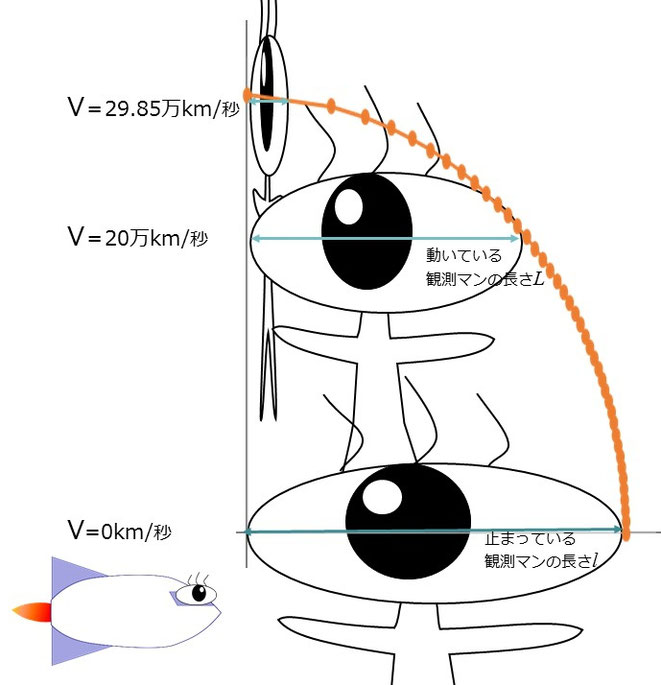
「縮んで見える」でした。
相手の立場で考えてみればいい。
ロケットから見たら、動いているのは観測マンなのだから。
これが相対性理論の「相対性」なのだ。
うまく説明できたかどうかわからないが、こんな感じでタイムマシンに関する物理学の理論や数式をいろいろ紹介していきたい。
※今回の記事を書く上でとても参考にさせていただいたのが広江克彦さんのサイト「EMANの物理学」。
こちららのサイトの内容は書籍でも出版されています。私のようなモニター画面よりも紙面の方が落ちつくという方は広江さんの著書「趣味で物理学」