●中学生や文系でもわかる!　アインシュタインの相対性理論E=mc2の数式解説

2018/11/2

タイムマシンやタイムトラベルの理論を考えるとき必ずといっていいほど登場するアインシュタインの特殊相対性理論の方程式E=mc²。

「世界で一番有名な方程式」であり、画期的な内容をシンプルな数式で表現したスマートさから「世界で一番美しい方程式」とも呼ばれている。

だがE=mc²が「何を意味しているのか？」、ましてや「どう導くのか？」になるとよくわからないという人も多いだろう。私もそうだった。

「何を意味するのか?」は一言でいえば「エネルギーは質量と同じもの」だが、「どう導くのか？」はいろいろな方法があって、さらにどれも簡単ではない。

けれどその中でも文系の私が一番わかりやすいおススメのE=mc²の導き方をご紹介したい。

※この「タイムマシンの物理学」は中学生や文系でもわかるわかりやすさを重視しており、基本的に中学生レベルの数学を使って紹介しているが、今回は1箇所だけ大学レベルの数学も使っている。

ただそれを理解しなければ進めないわけではないので、ご安心を。

まずは以前に紹介した「時間が遅くなる仕組みとは？」の復習から。

アインシュタインが1905年に発表した特殊相対性理論によると「時間（や空間）は相対的で変化するもの」で、「光の速度」は「唯一の変わらない速度」であり、光の速度に近づくほど時間の進み方が遅くなった。

この解説で使った「時間の遅れ」を計算する数式がこちらだ。

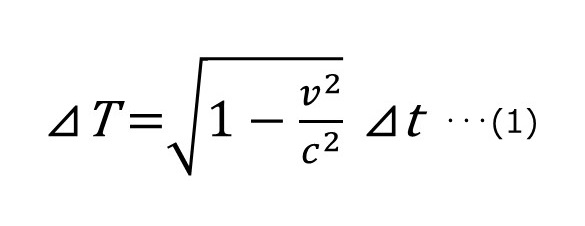
⊿（デルタ）は「ごくわずか」、tは「時間（time）」、vは「速度（velocity）」、cは「光の速度（constant/定数）」を意味する。

（速度変化を考えずにすむ）ごくわずかな時間ｔ（小文字）にルートの中をかけると、左のごくわずかな時間T（大文字）に変換されるという式だ。 

もう１つ、光の速度に近づくにつれて物体の長さが「縮む」数式もご紹介した。

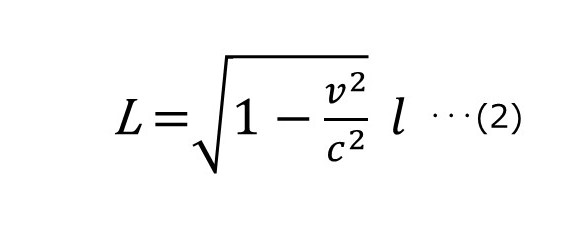
L（大文字）は「運動している物体の長さ（Length）」、vが「物体の速度」、cが「光の速度」、そしてｌ（小文字）が「静止している物体の長さ」を意味する。

ちなみにこの数式はオランダの物理学者ヘンドリック・ローレンツ（wiki）にちなんで「ローレンツ収縮」と呼ばれている。

この式を

出てきた係数（かける数）は、これまたローレンツにちなみローレンツ因子と呼び、ギリシア文字のγ（ガンマ）で表される。

このローレンツ因子γは後で重要な役割を果たすので覚えておいてほしい。

復習がすんだので、いよいよE=MC²を導いていこう。

さてここで、Aさんの乗った静止しているロケットに左右から光が当たっているシーンを考えてみよう。

光には質量はないがエネルギーを持っているので、左右どちらかの一方から光が当たるとロケットはその逆方向へ（ほんの微かだが原理的には）動いてしまう。

でもこのように両側から同時に光が当たると、エネルギーは相殺されてしまい、ロケットは動かない。

次にロケットが上方向へ一定の速度で動いているとする。

そしてロケットの外側から静止した状態で見ているBさんからロケットに当たる左右の光を見ると、

Bさんからは光が斜めに伸びてロケットに当たっているように見える。

ここで１つ疑問が生まれる。光は斜め下からロケットに当たっているように見えるので、光のエネルギーで押されてロケットは加速してしまうのではないか？

ところがロケットは加速しない。

ロケットを加速させるはずの光のエネルギーはどこに行ってしまったのか？

これを考えてみよう。

ここで重要なのは、エネルギーは、ある形態から他の形態へ変わっても、その総量は変わらないという「エネルギー保存の法則」（熱理学の第一法則）だ。

この法則に従えば、ロケットが動き出す前と一定の速度で動きした後のエネルギーの総量は同じなので、動いているロケットに当たって加速させるはずのエネルギーは何かに変わっているはずだ。

それを動いているロケットに当たる光のエネルギーから静止しているロケットに当たる光のエネルギーを引いて求めてみる。

運動するエネルギーEは、質量をｍ、物体の速度をvとして、 

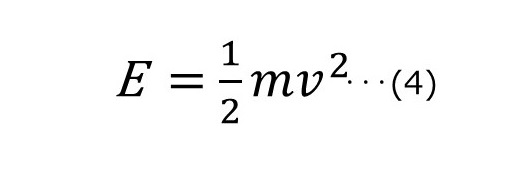
と表される。

静止しているときのAさんの乗ったロケットに左から当たる光のエネルギーをE/2、右から当たるエネルギーをE/2とすると、左右の合計は E/2 + E/2 ＝Eだ。

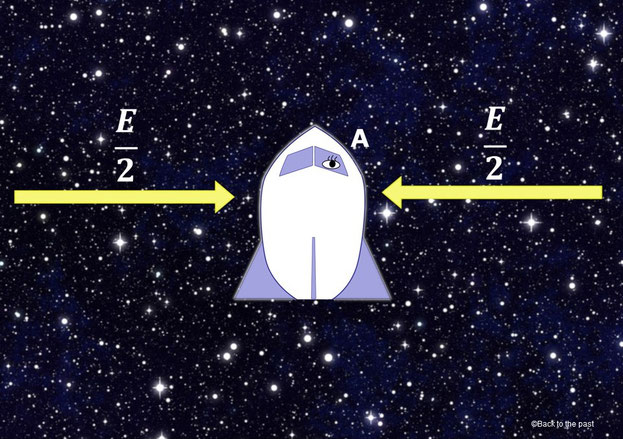
上方向へ動いているロケットに左右から当たる光は、ロケットの外側にいるBさんから見ると斜めに長くなり、この長くなった分を計算するために上で登場した(3)の式ローレンツ因子γを左右それぞれの光のエネルギーにかけてやる。

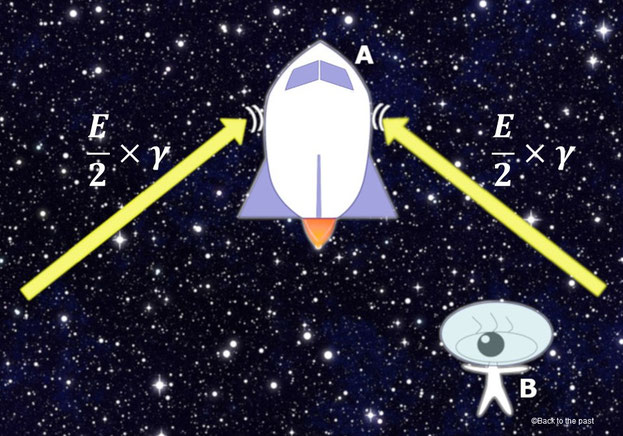
計算すると、左から当たるエネルギーE/2×γ、右から当たるエネルギーE/2×γを足して、（E/2×γ）+（E/2×γ）＝ E×γ となる。

そして動いているロケットに当たる光エネルギーの量 E×γ から静止したロケットに当たる光エネルギーの量 E を引くと、

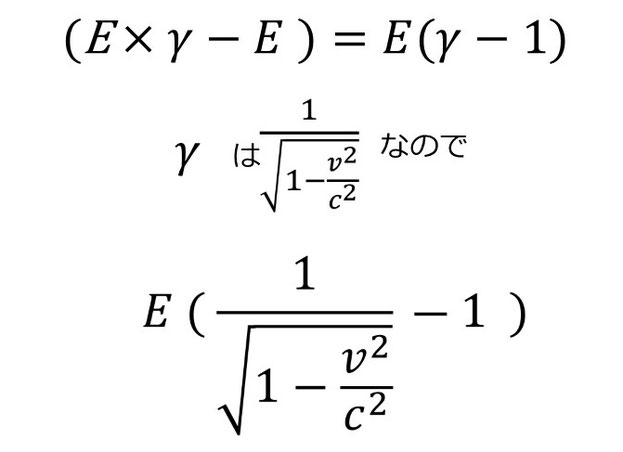
ここで「級数展開」という大学で習う数学のテクニックを使うと次のような式になり、

v＜c、つまり速度が光速度に比べて十分に小さいときは左から3番目の数より後はとても小さくなるので無視してしまうと、

という式になる。

ここで(5)の式と、(4)の運動エネルギーの式とを比べてみてほしい。

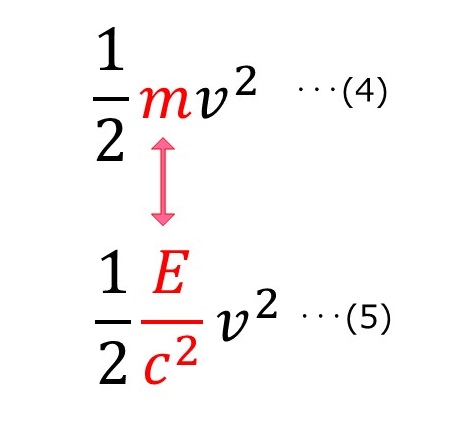
つまり(5)の式の E/c² は 質量 m と同じであり、ロケットに当たった光のエネルギーはロケットを加速させるのではなく、ロケットの重さを増やす質量になったのだ。

ここで E/c² と 質量 m を ＝ で結ぶと、

見事にE=mc²が導かれた！

さて E=mc²は質量mの物体が静止しているときのエネルギーだ。

速度vで動いているときはmc²にγをかけて

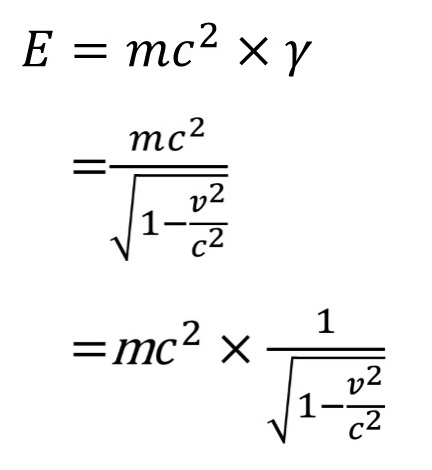
のように書く。

これは先ほどの級数展開を使って、

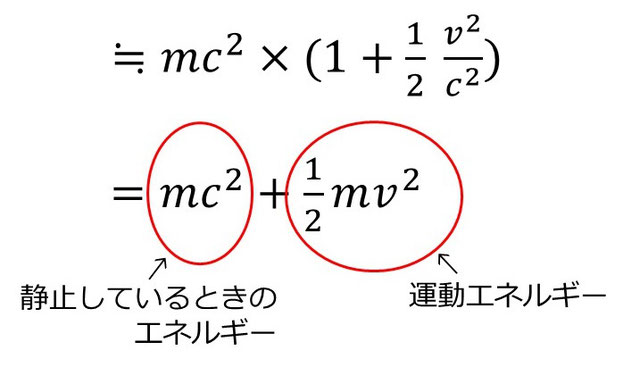
つまり、動いている物体は静止しているときのエネルギーと運動エネルギーの両方を持っている。

E=mc²の話をするときによく核爆弾のエネルギーが引き合いに出されるが、広島に投下された原子爆弾ですらあの爆発によって消えたウランの質量は総量のたった0.0014%にすぎなかった（E=mc²wikiより）。

通常の物質が逆の電荷をもつ反物質と対消滅すればその質量が100%のエネルギーに変換されるが、それがどれだけ莫大な量になるのかは想像もつかない。

人類がいつしかそのエネルギーを扱える日が来たとき、核爆弾のような兵器ではなく、夢のあるタイムマシンのエネルギー源として使ってほしい。